简介
Link/Cut Tree 是一种数据结构,用于解决动态树问题。
其又称 Link-Cut Tree,简称 LCT,但不叫动态树。动态树指一类问题。
“Splay” 是 LCT 的基础,但 LCT 中的 Splay 在细节处不太一样,进行了一定的扩展。
这是一个和 Splay 一样只需要几个核心函数就能实现一切的数据结构。
问题引入
维护一棵树,在线询问,支持如下操作:
- 修改两点间路径权值
- 查询两点间路径权值和
- 查询子树权值和
- 修改子树权值
- 断开并连接一些边,保证仍然是一棵树
如果没有最后一个操作,就是轻重链剖分的模板题。
而有了最后一个操作,就是动态树问题。可以使用 LCT 求解。
什么是动态树问题?
- 维护一个森林,支持删边、加边,保证操作后仍是森林,维护有关信息。
- 一般的操作有两点连通性、两点路径权值和、连接两点、切断某条边、修改信息等。
我们回忆一下,如果没有修改树的形态的操作,轻重链剖分是如何解决此类问题的。
- 对整棵树按子树大小进行剖分,重新标号。
- 重新标号后,在树上形成了若干以链为单位的连续区间,可以用支持区间操作的数据结构进行修改。
那么转向动态树问题,我们希望能指定一种剖分方式,让这个链式我们需要的链。
实链剖分
实链剖分是一种动态的剖分方式。
对于一个点连向它儿子的所有边,我们选择一条边进行剖分。
被选择的边称为实边,其他边为虚边。
实边连接的儿子称为实儿子。
对于一条实边连接成的链,称为实链。
实链剖分的剖分结果是可变的,可以灵活调整。
我们使用 Splay 来维护实链。
LCT
感性地说,LCT 利用若干 Splay 来维护动态的树链剖分,以期实现动态树上的区间操作。
对于每条实链,建立一棵 Splay 来维护整条链的信息。
辅助树(Auxiliary Tree)
性质
每棵辅助树维护的是对应的一棵原树。
若干辅助树组成了 LCT,而 LCT 维护对应的森林。
辅助树由多棵 Splay 组成,每棵 Splay 维护原树中的一条路径(实链)。
中序遍历某棵 Splay,得到的点序列,对应于原树从上到下访问这条路径得到的点序列。
换句话说,Splay 中的点的排序权值是其在原树中的深度。我们不会显式地指定权值。
原树中的节点与 Splay 节点一一对应。
辅助树的各棵 Splay 并不是独立的,每棵 Splay 的根节点的父亲节点指向该实链顶端节点的父亲节点对应的 Splay 节点,这样就可以实现跳链的功能。
注意,这里儿子认父亲,父亲不认儿子。其对应的是原树上的虚边。
具体地,可以从某条实链获取其上一条实链的信息,却不能实现获取下一条实链的信息。
这是因为父亲是唯一的,而儿子不是。
那么,每个联通块恰好有一个点的父亲节点为空。
由于辅助树的以上性质,我们在任何时刻都不需要维护原树,而可以通过辅助树得到唯一的原树。
所以我们只要维护辅助树即可。
可以发现,辅助树中每棵 Splay 起到的作用,类似于轻重链剖分中的线段树。
不同点在于,轻重链剖分中,利用同一棵线段树完成了原树的信息统计,每条重链对应线段树上的一个区间。
而在辅助树中,利用若干棵 Splay 完成了原树信息的统计,每条实链对应一棵 Splay.
现在我们有一棵原树,其中实线为实边,虚线为虚边。
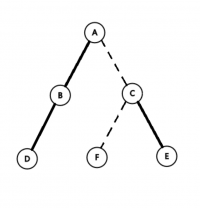
那么由刚刚的定义,可以得到其辅助树:
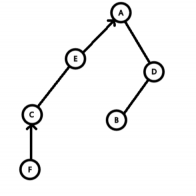
原树与辅助树的关系
原树中的实链,在辅助树上属于同一棵 Splay.
原树中的虚边:在辅助树上,子节点的父亲指针指向父亲,但父节点的两个儿子指针都不指向儿子。
原树中的根可以与辅助树的根不同。
原树中的父子关系可以与辅助树中的父子关系不同。
辅助树可以在满足其性质前提下,利用 Splay 操作任意换根。
虚实链变换可以在辅助树上轻松完成,这就实现了动态树链剖分。
实现
首先声明一些变量的含义:
to[maxn][2],左右儿子。fa[maxn],父亲。sum[maxn],路径权值和,即 Splay 中的子树权值和。val[maxn],点权。tag[maxn],翻转标记。lazy[maxn],权值标记,对应区间加。siz[maxn],辅助树上子树大小- ……
声明一些函数的意义:
pushup(x),上推操作,维护信息。pushdown(x),下推操作,维护信息。get(x),对应 Splay 中获取父子信息,即获取 $x$ 是父亲的哪个儿子。rotate(x),Splay 中的旋转操作,将 $x$ 向上旋转一层。splay(x),Splay 中的 Splay 操作,将 $x$ 旋转到根。access(x),将原树上根到 $x$ 中的所有点放在一条实链中,使根到 $x$ 成为一条实链,并且在同一棵 Splay 中。本操作是 LCT 的核心。isroot(x),判断 $x$ 是否是所在的 Splay 的根。update(x),在access操作后,递归地从上到下pushdown更新信息。makeroot(x),使 $x$ 成为其所在的树的根。link(x,y),在 $x$ 点与 $y$ 点之间加一条边。cut(x,y),删除 $x$ 点与 $y$ 点之间的边。find(x),找到 $x$ 所在的树的根节点编号。fix(x,k),将 $x$ 的点权修改为 $k$ .split(x,y),提取出 $x$ 点与 $y$ 点之间的路径,方便区间操作。
一般来说,还会宏定义 ls 为 to[x][0],定义 rs 为 to[x][1].
函数详解
pushup
|
|
pushdown
|
|
get
判断是否为右儿子,与 Splay 中一致。
|
|
isRoot
判断当前点是否是当前 Splay 的根,具体地,如果它是当前 Splay 的根,那么其父亲的左右儿子都不是它。
|
|
rotate
旋转函数,和 Splay 大体相同,但有一处需要注意的点。
|
|
splay
|
|
access
核心功能。将原树上的根到 $x$ 的路径变成实链。先给出代码,再详细解释。
|
|
可以发现,代码非常简短,也非常难以理解。
让我们更具体地描述 access 操作的目的:将根到 $x$ 的路径上的点放在同一棵 Splay 中,同时让原本 $x$ 的实儿子不再留在 Splay 中。
一次 access 做了如下操作:
- 将当前指针节点旋转到根。
- 把儿子换成之前的节点。
- 更新当前点的信息。
- 指针向上。
还有一个返回值,这个返回值是什么意思呢?
最后一次虚实链变换时虚边父亲节点的编号。
- 连续两次
access操作时,第二次操作的返回值是这两个节点的 LCA. - 表示 $x$ 到根的链所在的 Splay 的根。这个节点一定已经被旋转到了根节点,且父亲一定为空。
为什么这样就能让根到 $x$ 的所有边变成实边呢?
我们一路旋转向上,所经过的每个点都被转到根,并且都与上一个在根的点用实边相连。
也就是说,每个点都抛弃了它原先的右儿子,而将原本以虚边连接的路径上的上一个点设置为右儿子。
我们结合一个例子来理解:

其对应的辅助树可能长这样:
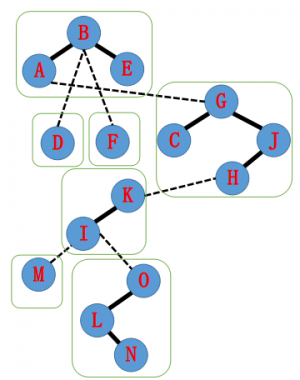
其中每个绿框中都是一颗 Splay.
在第一次操作中,我们将 $N$ 点旋转到根,并且抛弃其右儿子 $O$ .
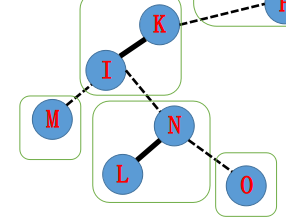
第二步,我们将 $I$ 旋转为根,同时抛弃其原本的右儿子 $K$ ,而连接上 $N$ 作为右儿子。
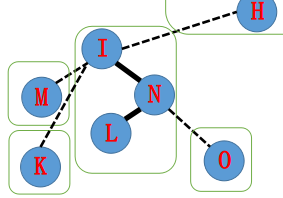
下一步,将 $H$ 旋转到根,并将 $I$ 作为右儿子:
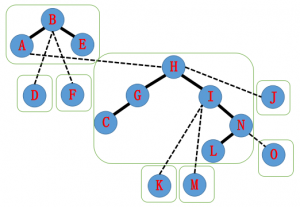
最后将 $A$ 旋转到根,并将 $H$ 作为右儿子:
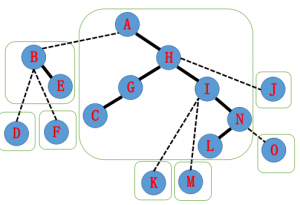
这就完成了一次 access 操作!
让我们再想想为什么可以成功:
- 一棵 Splay 的根到其父亲的边,一定对应原树上的一条虚边。
- 那么一棵 Splay 的根的父亲就是其在原树上的父亲。
- 我们跳到这条实链的顶端节点的父亲上,并将原先的虚边变成实边,依次操作,就能连接出一条实链。
- 为什么连接右儿子?因为根据辅助树的性质,其中序遍历对应原树上的遍历,那么原树上的儿子应该当辅助树上的右儿子。
update
下推标记。
|
|
makeroot
该函数的重要性不低于 access.
我们在维护路径信息时,会出现路径深度无法严格递增的情况。
根据辅助树的性质,这种路径是无法出现在一棵 Splay 中的。
那么此时我们需要用到 makeroot 函数,其作用是使点 $x$ 成为原树的根。
设 access 的返回值为 $y$ ,此时 $x$ 到根的路径恰好构成一棵 Splay.
如果将树用有向图画出来,给每条边定方向为儿子到父亲的方向。
那么换根到 $x$ 相当于,将当前根到 $x$ 路径上的边全部反向。
我们知道,目前的一棵 Splay 的中序遍历代表其在原树上的遍历。
因此我们只需要翻转当前根到 $x$ 的路径的 Splay,就能实现其在原树上的遍历的翻转,也就是翻转了对应的边。
|
|
link
连接点 $x$ 与 $y$ ,先 makeroot(x),然后令 $x$ 的父亲为 $y$ 即可。
注意这个操作不能发生在同一棵树内,因此有时需要判断连通性。
|
|
split
拿出一棵 Splay,其维护的是 $x$ 到 $y$ 的路径。
先 makeroot(x),然后 access(y),就可以得到对应的路径了。 如果需要 $y$ 做根,还可以 splay(y).
cut
如果保证合法,直接 split(x,y),此时原树上 $x$ 为根,辅助树上 $y$ 为根,那么 $x$ 在辅助树上一定是 $y$ 的左儿子,直接断开即可。
|
|
如果不保证合法,需要满足三个条件:
- $x$ 与 $y$ 连通。
- $x$ 与 $y$ 路径上没有其他链。
- $x$ 没有右儿子。
上面三个条件保证了 $x$ 与 $y$ 之间有边。
判断连通需要用到后面的 find 函数,而其余两个很好实现:
|
|
find
找到当前辅助树对应的原树的根。
在 access(x) 后,再 splay(x),这样根就是该 Splay 中的最小值,根据"二叉搜索树"性质,一路走左儿子即可。
注意过程中下推标记,注意最后把根 splay 上去保证复杂度。
|
|
fix
修改某个点的点权,直接将其辅助树的根,这样修改它的点权就只会影响它自己了。
|
|
至此,我们的函数详解完成了!一路看下来,你已经完成了 $14$ 个函数的学习!
注意
有一些需要注意的点:
- 一定记得
pushup与pushdown,非常重要。 - LCT 中的
rotate需要先判断isroot,所以连接父亲的父亲的关系的语句在最前面。 - LCT 中的
splay就是旋转到根,不需要旋转到儿子。 - 建树时,可以默认所有边为虚边,直接只指定父亲关系。
pushdown 翻转
一般来说,有两种翻转标记的写法。
一种写法是,当前点有翻转标记,代表当前点的左右儿子未翻转,但需要翻转。
这种写法我个人比较常用。
用这种写法,在从上往下遍历时,需要先下推,再判断左右儿子。
|
|
另一种写法是,当前点有翻转标记,代表当前点左右儿子已经翻转,并且左右儿子也要翻转。
这种写法更加接近线段树中的标记的写法,在需要从上往下下推标记时也比较自然。
应用
维护树链信息
LCT 通过 “split” 操作,可以将树上 $x$ 点到 $y$ 点的路径提取到一棵 Splay 中,树链信息的修改和统计转化为平衡树上的操作,这让 LCT 在维护树链信息上具有优势。
此外,借助 Splay 的链上二分比轻重链剖分少一个 $\log$ 的复杂度。
对树上路径 $(u,v)$ 进行修改时,先 split(u,v).
其他的都是 Splay 上的操作了。
例题详见 “LCT 练习笔记”.
维护连通性质
维护是否连通
借助 find 函数就可以维护动态森林的连通性了。
维护边双连通分量
维护边权
LCT 不能直接处理边权,因此需要利用虚点来维护边权。
具体地,对每条边建立一个虚点,虚点用两条边连接其原本的起点、终点即可。
维护子树信息
LCT 不擅长维护子树信息。